Datenanalyse: Carcassonne
By Philipp Leppert in R Freizeit
December 13, 2017
Carcassonne ist ein Brettspiel für 2-4 Spieler bei dem abwechselnd zufällig gezogene Plättchen an das bestehende Spielfeld angelegt werden. Um Punkte zu sammeln, müssen die Spieler auf dem aktuell ausgelegten Plättchen eines ihrer sog. Meeple platzieren und so eine Burg, Straße, Kloster oder Wiese für sich zu beanspruchen. Von einem Spieler beanspruchte Gebiete können allerdings von einem Mitspieler durch geschicktes Anlegen und Platzieren der Meeple streitig gemacht werden.
 |
|---|
| Eine Partie Carcassonne. Eigene Aufnahme. |
Datenbeschaffung
Zwischen September 2016 und Oktober 2017 habe ich nach jeder Partie den Endpunktestand von mir und meiner Freundin erfasst. Im Folgenden wird also lediglich die 2-Spieler Variante betrachtet, deren Dynamik sich recht deutlich vom Spiel mit 3, 4 oder 5 Personen unterscheidet. Es wurden insgesamt 124 Runden aufgezeichnet. Gleichzeitig wurde auch für jede Spielrunde festgehalten, wer das Spiel eröffnet hat und die Differenz der Endpunktestände berechnet.
Datenanalyse
Zunächst einige Eckwerte des Carcassonne-Datensatzes: Philipp erzielte im Durchschnitt etwa 7 Punkte mehr als Claudia und errang auch gleichzeitig das höchste Gesamtergebnis mit 143 Punkten (juhu). Claudia hingehen erzielte den niedrigsten Punktestand mit 58 Punkten (sorry). Die höchste Punktedifferenz in einem Spiel betrug 68 Punkte. Insgesamt gewann Philipp 80 Runden und musste sich 42 Mal geschlagen geben. Zwei Runden endeten mit einem Unentschieden.
## Punkte_Philipp Punkte_Claudia Differenz
## Min. : 69.0 Min. : 58.00 Min. : 0.00
## 1st Qu.: 92.0 1st Qu.: 88.00 1st Qu.: 6.00
## Median :105.0 Median : 98.00 Median :14.00
## Mean :105.4 Mean : 97.91 Mean :18.52
## 3rd Qu.:118.0 3rd Qu.:108.00 3rd Qu.:27.25
## Max. :143.0 Max. :132.00 Max. :68.00
##
## Claudia Philipp Unentschieden
## 42 80 2
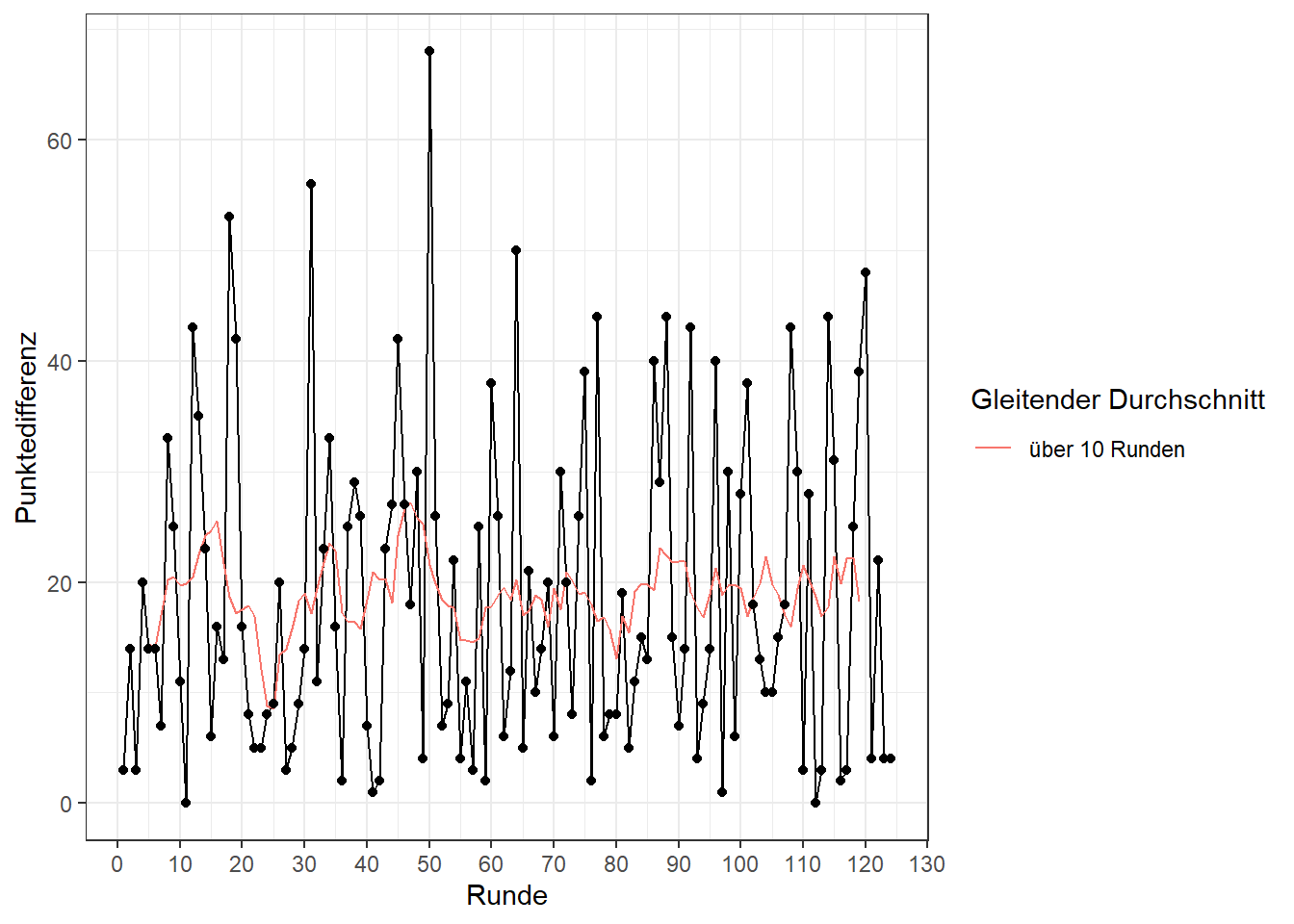
Die folgende Grafik zeigt den Puntkeunterschied über alle gespielten Runden. Der gleitende Durchschnitt über 10 Runden ist in Orange dargestellt. Mal gingen die Spiele recht knapp aus, mal ging ein Spieler als deutlicher Sieger hervor. Im Mittel bewegt sich die Differenz der Punktstände um 19 Zähler.
ggplot(carcassonne, aes(Runde, Differenz)) +
geom_line() +
geom_line(aes(y=rollmean(Differenz, 10, na.pad=TRUE),color="red")) +
geom_point() +
scale_color_discrete(name="Gleitender Durchschnitt", lab="über 10 Runden") +
labs(y="Punktedifferenz") +
scale_x_continuous(breaks = c(seq(0,130,10)))
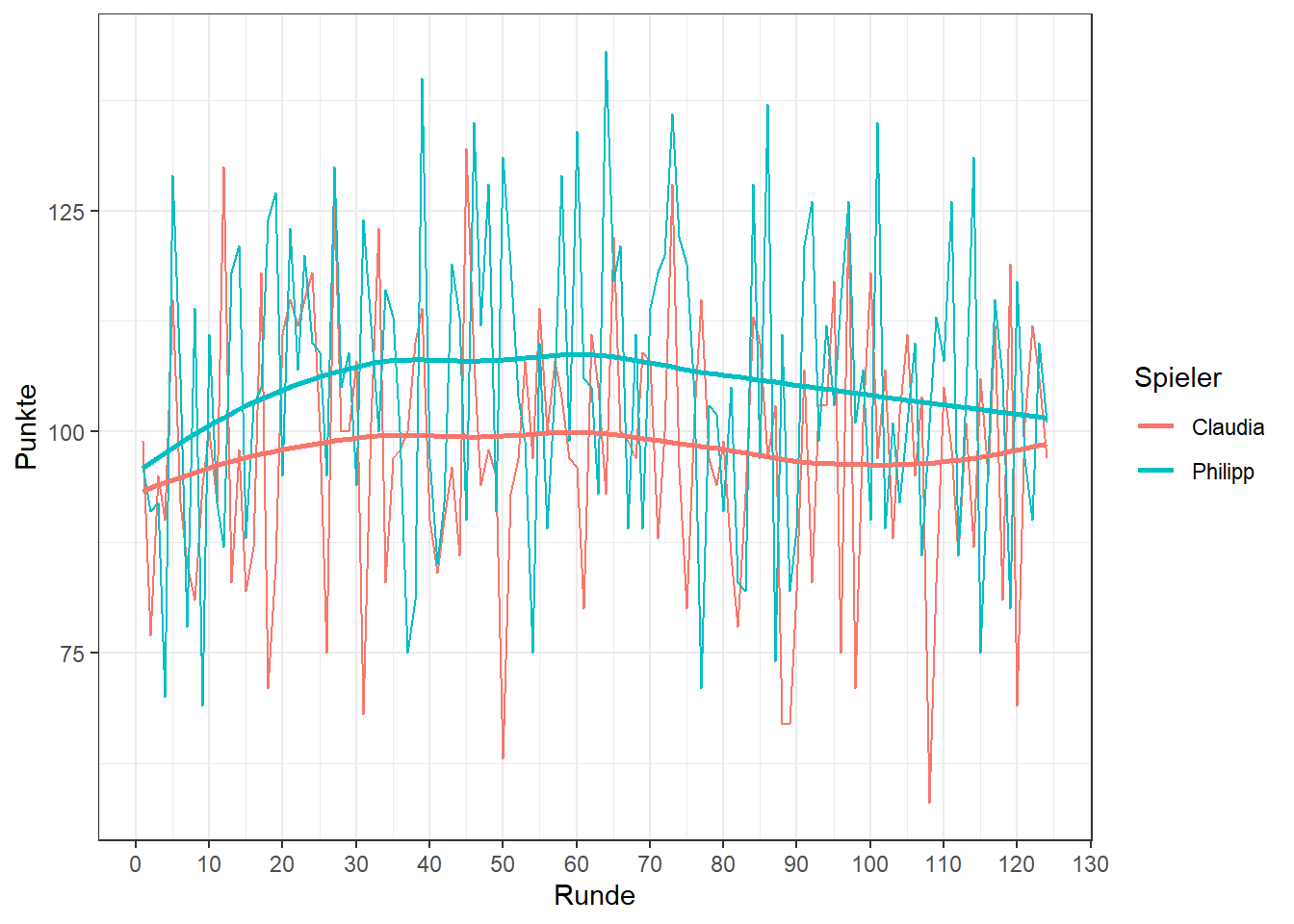
Betrachtet man den Gesamtpunktestand jedes Spielers in der nächsten Darstellung im Zeitverlauf, so kann Philipp bis zur 60. Partie sein Ergebnis im Durchschnitt verbessern. Danach ist dieser Trend allerdings wieder rückläufig und der Endpuntkestand verschlechtert sich. Auch bei Claudia ist dieser anfängliche Trend zu erkennen.
carcassonne %>%
gather(key="Spieler", Punkte, Punkte_Philipp, Punkte_Claudia) %>%
ggplot(data=., aes(x=Runde, y = Punkte, col = Spieler)) +
geom_line() +
geom_smooth(se = F) +
scale_color_discrete(lab=c("Claudia","Philipp")) +
scale_x_continuous(breaks = c(seq(0,130,10)))
Erhält ein Spieler einen Vorteil, wenn er das Spiel eröffnen darf? Dazu verwende ich ein lineares Regressionsmodell in dem jeweils Philipps bzw. Claudias Endpunktestand als abhängige Variable definiert wird. Der Startspieler-Vorteil wird als binäre Variable in das Modell eingefügt und als weitere Kontrollvariable wird der Punktestand des gegnerischen Spielers verwendet. Die beiden Modelle sehen so aus:
# Modell Philipp
lm_p <- lm(Punkte_Philipp ~ factor(Startspieler) + Punkte_Claudia, data = carcassonne)
# Modell Claudia
lm_c <- lm(Punkte_Claudia ~ factor(Startspieler) + Punkte_Philipp, data = carcassonne)
Die Ergebnisse der beiden Modelle sind unten abgebildet. Eröffnet Philipp das Spiel hat dies einen positiven, aber nicht signifikanten Einfluss auf seinen Endpunktestand. Der Endpunktestand von Claudia ist dagegen um 7 Punkte signifikant niedriger, wenn Philipp das Spiel eröffnet. Womöglich leidet hier die Moral, wenn sich Philipp beim Auftakt die erste Burg sichern kann.
Modell Philipp:
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 101.80 | 11.02 | 9.24 | 0.00 |
| factor(Startspieler)Philipp | 3.02 | 3.13 | 0.96 | 0.34 |
| Punkte_Claudia | 0.02 | 0.11 | 0.20 | 0.84 |
Modell Claudia:
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 99.78 | 8.26 | 12.08 | 0.00 |
| factor(Startspieler)Philipp | -7.00 | 2.60 | -2.69 | 0.01 |
| Punkte_Philipp | 0.02 | 0.08 | 0.20 | 0.84 |